Las Matemáticas

Tales de Mileto (s. VI a.n.e ) Euclides (s. IV-III a.n.e) 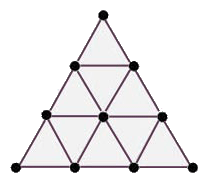Tetractys 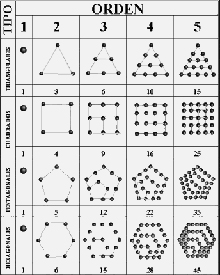Números poligonales 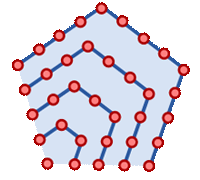Números pentagonales Polígonos regulares

Es muy probable que tanto Tales de Mileto como Pitágoras de Samos no se iniciaran en el conocimiento de la aritmética y la geometría hasta que viajaron por Egipto, Babilonia y Fenicia, donde existía una tradición matemática muy antigua. Hacia el año 2000 a.n.e. los escribas sumerios y egipcios ya sabían calcular áreas y volúmenes a partir de longitudes. Al menos desde el año 1500 a.n.e. circulan en ambos imperios textos escolares que plantean y resuelven problemas matemáticos, como hallar raíces cuadradas o calcular la altura de una pirámide conociendo su lado y su pendiente. El saber aritmético y geométrico era muy apreciado para la formación de los funcionarios imperiales que se ocupaban de la administración, por ejemplo, para inventariar los bienes del Estado y calcular los impuestos de los súbditos.

La principal diferencia entre las matemáticas egipcias y babilonias, por un lado, y las griegas, por otro, es que las primeras eran meramente empíricas, destinadas a funciones prácticas, como medir campos o determinar tributos, conformándose con obtener reglas para alcanzar los objetivos buscados o con encontrar los resultados concretos para los problemas que se planteaban. En cambio, la última muestra desde sus orígenes su vocación teórica, su afán por fundamentar aquello que se afirma: de ahí surgen los conceptos de prueba, demostración, axioma y teorema. Ello va a permitir emprender el camino desde unas matemáticas donde se halla mezclado lo empírico y lo teórico, como en Tales de Mileto o en las primeras generaciones de pitagóricos, hasta unas matemáticas abstractas, que sólo se alcanzan y consolidan definitivamente en la época de la Academia de Platón, cuando se teoriza la existencia de entes no materiales, como el espacio, los números y las formas, alcanzando su apogeo en el siglo III a.n.e. con los Elementos de Euclides, obra que sistematiza buena parte de la matemática anterior, y con el genio incomparable de Arquímedes de Siracusa.

En la época inicial, siglo VI a.n.e., con Tales de Mileto, a quien casi todas las fuentes citan como el fundador de la matemática griega, la visualización tenía gran importancia a la hora de probar las tesis. Ocurría en la geometría, como se comprueba al ver la influencia de la simetría en los teoremas atribuidos a Tales, y ocurría en la aritmética, donde los números solían ser representados mediante guijarros, formando figuras determinadas: son los llamados números figurados o poligonales.

Esa era la situación en los primeros tempos de la secta pitagórica y algunas de las demostraciones del teorema de Pitágoras tienen un componente práctico-visual. Pero será mérito de los matemáticos pitagóricos avanzar rápidamente hacia la noción abstracta de número, punto, línea y figura. Según la mayoría de los historiadores también corresponde a los pitagóricos el mérito de haber realizado las primeras demostraciones puramente formales y haber consolidado la demostración como el método de las matemáticas. Habría ocurrido con su teoría de los números pares e impares, elaborada a mediados del siglo V a.n.e., que sería recogida por Euclides en sus Elementos. Otros historiadores ven el comienzo del método demostrativo en la obra de Parménides de Elea, filósofo itálico de esa misma época que critica al pitagorismo.

De por entonces son los primeros textos griegos que recopilan los conocimientos alcanzados hasta entonces, presentándolos de manera ordenada y útil para el aprendizaje; esos textos serán conocidos por el nombre de “Elementos”. Alguna de esas obras es de procedencia pitagórica, aunque el primer nombre propio conocido como autor de unos Elementos fue Enópides de Quíos.

La Aritmética

Para los pitagóricos lo Uno, la Unidad, es la fuente de todos los números; por eso para ellos el uno no es un número, sino el origen de lo par y lo impar, que son los dos principios constituyentes de los números; por tanto, no es extraño que no inventaran el cero, puesto que al igual que el uno ni cuenta nada ni mide nada. Los pitagóricos –y luego todos los matemáticos griegos- sólo consideran como números a los naturales; nuestros números fraccionarios son para ellos relaciones entre números, a las que llamarán “logos”, razones; a su vez, la relación entre dos razones será llamada analogía, proporción. La consideración de los números como un conjunto formado por adición de unidad en unidad se atribuye al pitagórico Eurito, a finales del siglo V a.n.e. La importancia de los números para los pitagóricos hizo que tomaran como símbolo sagrado la tetraktys, que representa los diez primeros números en forma de triángulo equilátero.

Algunos historiadores llaman a la aritmetica pitagórica “aritmogeometría”, porque expresaban los números en forma de figuras geométricas, los números “poligonales”, que dan lugar a series como los números triangulares (3, 6, 10, 15…), los números cuadrados (4, 9, 16, 25…), los números pentagonales (5, 12, 22, 35…), los números hexagonales (6, 15, 28, 45…) y así sucesivamente.

La Geometría

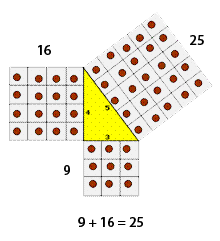
La geometría pitagórica es una geometría material, un saber acerca de los cuerpos reales. El punto es la unidad geométrica, definido como “unidad dotada de posición”. A partir de él se generan las dimensiones físicas: líneas con longitud, superficies con extensión, sólidos con volumen. El teorema de Pitágoras, que afirma que la suma de las áreas de los cuadrados construidos sobre los catetos de un triángulo rectángulo es igual al área del cuadrado construido sobre la hipotenusa, era conocido en Egipto y usado por los agrimensores, pero los pitagóricos fueron los primeros en aportar una demostración, similar probablemente a la que expone Euclides en sus Elementos, Vl, 31.

La determinación de áreas es uno de los problemas clásicos de la geometría pitagórica y puede enunciarse así: Dadas dos figuras determinar una tercera figura de área igual a la primera y forma semejante a la segunda. Algunas de estas construcciones y demostraciones quedaron recogidas siglos después en los libros I y II de los Elementos de Euclides. El estudio de las variantes de este problema condujo al conocimiento de la semejanza y relaciones entre las figuras rectilíneas. De ahí surge el concepto de “media proporcional”: Dados un cuadrado y un rectángulo de igual área el lado del cuadrado es media proporcional entre los lados del rectángulo.

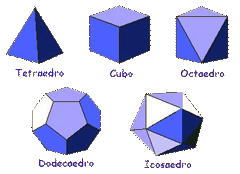
Seguramente los pitagóricos conocían ya los cinco sólidos regulares, o sea, que tienen todos sus lados, caras y ángulos iguales: tetraedro, cubo, octaedro, dodecaedro e icosaedro. Sabemos que los pitagóricos intentaban formar figuras empíricamente juntando ángulos en torno a un punto. Así uniendo cuadrados de 3 en 3 surge el cubo. Uniendo triángulos equiláteros de 3 en 3, de 4 en 4 y de 5 en 5 surgen, respectivamente, el tetraedro, el octaedro y el icosaedro. El dodecaedro es una figura formada por 12 pentágonos regulares; ésta era un polígono de gran interés para los pitagóricos porque su lado y su diagonal se encuentran en razón áurea, o sea, la proporción entre el uno y la otra es igual que entre la otra y la suma de ambos: a/b = b/a+b.

Actividades

1. Buscar algún problema matemático formulado en los papiros egipcios o en las tablillas mesopotámicas, formularlo al modo actual y resolverlo.
2. Averiguar los nombres de tres matemáticos entre los que trabajaron en la Academia de Platón.
3. Buscar al menos dos teoremas matemáticos que se atribuyan a Tales de Mileto.
4. Exponer alguno de los teoremas pitagóricos sobre los números pares e impares recogidos en los Elementos de Euclides.
5. Averiguar cuál es el quinto número triangular, el décimo número cuadrado y el quinto pentagonal.
6. Investigar a qué se llama “los tres problemas clásicos de la matemática griega”.
7. Buscar el valor de la superficie de las caras de un tetraedro de lado uno.
8. Buscar el valor de la diagonal de un pentágono regular de lado uno.
9. Averiguar la fórmula del volumen de un octaedro.
10. Investigar qué aspectos de la vida humana simbolizaban para los pitagóricos algunos de los números de la tetraktys.

Para saber más

• Pitágoras. El filósofo del número. González Urbaneja, Pedro. Editorial Nivola.
• La ciencia y el milagro griego. Babini, Jose. Centro Editor de América Latina.
• El Teorema de Pitágoras.Claudi Alsina. Editorial RBA.
• Pitágoras y su teorema. Strathern, Paul. Editorial Siglo XXI.
• El mundo físico de los griegos, Samuel Sambursky, Alianza Editorial, véase el capítulo primero.