El sentido de las matemáticas en la filosofía de Platón

Las matemáticas en Grecia antes de Platón

Platón Eudoxo de Cnido Fragmento de "República" Mosaico griego representando una escena en la Academia de Platón 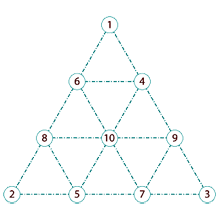Tetractys Pitágoras de Samos Fragmento del libro II de los "Elementos de Euclides" conteniendo la Proposición V (c. 100 a.n.e.) Ciudad de Atenas en la época de Platón

La gran aportación de los matemáticos griegos fue transformar el saber empírico de civilizaciones anteriores, como la mesopotámica o la egipcia, en una matemática teórica, es decir, en un saber que prueba o demuestra sus construcciones por deducción a partir de un conjunto de axiomas, postulados y definiciones. Ese proceso se inicia con Tales de Mileto y Pitágoras de Samos, tiene un punto de inflexión en la Academia de Platón y alcanza su forma canónica con los Elementos de Euclides de Alejandría. Los números y las figuras serán considerados como entidades ideales independientes de aquello a lo que remiten: las cosas contadas o figuradas. Esa idealización implica un camino de lo concreto a lo abstracto, de la percepción visual a la comprensión racional.

La práctica matemática y su transmisión cultural obligaron desde muy pronto a depurar los conceptos y principios utilizados, para enfrentar las críticas de los escépticos. Será el éxito de las matemáticas, y en particular el triunfo del método deductivo, lo que convierta a este saber en el modelo del conocimiento verdadero. Este periplo matemático no deja de verse afectado por condicionantes culturales, tanto religiosos y filosóficos como políticos.

En los orígenes de la matemática griega sus conceptos remiten a las cosas reales, no son todavía entes ideales. Una prueba clara del vínculo de los números con las cosas es que durante siglos ni los matemáticos ni los filósofos helenos pensarán los números como ilimitados. En efecto, los griegos consideran el universo como limitado, por lo que los números, que cuentan las cosas, no pueden serilimitados ya que no hay ilimitadas cosas. Para ellos los números sólo existen cuando están contando algo, no como pura especulación mental o mera acumulación de signos. Todavía Platón, para quien contar es tan básico e importante que no considera hombre a quien no conoce los números, se pregunta en su diálogo Parménides, escrito hacia el 360 a.n.e., si el número no es esencialmente ilimitado, pero opta por considerar que los números de la década generan todos los números, siguiendo una doctrina pitagórica.

En lo que se refiere a los entes geométricos inicialmente se consideraba a los puntos, las líneas, las superficies y los sólidos como figuras reales existentes en las cosas, hasta que el proceso de idealización fue convirtiendo al punto en algo sin dimensión, a la línea en longitud sin anchura, a la superficie en plano sin espesor y al sólido en un volumen espacial ideal. Platón se negará a conceder existencia real al punto, definiéndolo simplemente como el nombre que se da a los extremos de una línea; en cambio a las líneas, las superficies y los sólidos sí les otorga una existencia real porque tienen magnitud.

En algunos diálogos de Platón, donde imagina polémicas entre Sócrates y sus interlocutores para alcanzar un consenso acerca de temas importantes, aparecen algunos sofistas, a quienes el autor –gran paladín de la matemática idealizada- execrará acusándolos de confundir los números abstractos o las figuras geométricas ideales con las apariencias físicas sensibles; pero más bien se trata de que se mantienen fieles a una opción diferente y tradicional, la de las matemáticas apegadas a lo real.

Aunque Platón no fuera un matemático de relieve, en sus obras toma una posición clara respecto a la cuestión ontológica. Los números y las figuras son entidades ideales, inteligibles, eternas, inmutables, independientes y separadas de los seres naturales. En sus obras las matemáticas se reafirman en la dimensión cosmológica y sagrada adquirida con los pitagóricos, yendo incluso “hyperouranos”, más allá de los cielos. Los números y figuras son los principios eternos que gobiernan la Naturaleza cambiante y mortal. Las matemáticas expresan el orden de la necesidad, la verdad sobre el mundo, comprensible solo por el alma racional, no por el cuerpo sensible. Al final de su vida llegó a proponer como religión popular de la polis racional ideal una teología astral que se fundaba en la astronomía matemática.

La Academia y la Teoría de las Formas o Ideas

La creación por Platón de la Academia, hacia el 387 a.n.e., que reúne a un buen grupo de estudiosos para trabajar en común, va a facilitar el trabajo de producción, acumulación y debate intelectual en campos que hoy llamamos astronomía, matemáticas, cosmología o filosofía. El lema que la presidía “Nadie entre aquí que no sepa geometría” manifestaba con rotundidad la importancia que se otorgaba a ese saber. Trabajarán en ella matemáticos de renombre como Teeteto de Atenas, a quien se atribuye buena parte de los libros X y XIII de los Elementos de Euclides, y Eudoxo de Cnido, quien con su teoría de las proporciones y su método de exhaución, recogidos en los libros V y XII de los Elementos, solucionará el tratamiento de las magnitudes inconmensurables, y otros geómetras cuya obra no ha perdurado, como Leodamas de Thasos y Neoclides. Además, en sus viajes a Sicilia, Platón recibirá la influencia de importantes matemáticos pitagóricos, a través de los escritos cosmológicos de Filolao y de los trabajos en geometría y mecánica de Arquitas de Tarento. Es posible que fuera el propio Platón quien pidiera a Eudoxo, la elaboración del primer modelo matemático del movimiento de los astros: la teoría de las esferas homocéntricas, formulado por el astrónomo hacia el 355 a.n.e.

En las matemáticas se halla el origen y fundamento de la teoría platónica de las formas o ideas. En esta la idealización de los entes matemáticos se transforma en la idealización de los entes físicos y psíquicos. La verdad matemática, por su invariabilidad en el tiempo, era el modelo a seguir en todo conocimiento intelectual. El método deductivo, que partiendo de axiomas y definiciones llegaba a la demostración de teoremas, era el modelo prestigioso de razonamiento para todo saber. En el diálogo Menón Sócrates, a través de preguntas y respuestas, hace que un esclavo alcance por su propio razonamiento una verdad matemática; así, de una manera popular, expone Platón que las matemáticas están en el alma humana, ya que en esta se halla presente el logos que gobierna el mundo material mediante las proporciones aritméticas y geométricas. Sólo se requiere la introspección para volvernos conscientes de ese saber interno.

Con la teoría de las Formas o Ideas Platón pretende explicar la existencia de los seres naturales como copias de arquetipos únicos que existen más allá del mundo físico. Cada conjunto de seres naturales semejantes, que conocemos mediante los sentidos y denominamos con un mismo concepto, deben su existencia y sus características comunes a su Forma arquetipo, que puede ser conocida exclusivamente mediante la razón. En sus diálogos de juventud dice que hay formas de diverso tipo: de las especies naturales, de las virtudes morales, de los conceptos matemáticos. Más tarde, en República, al plantear la división entre seres sensibles e inteligibles, Platón expone que estos últimos son de dos tipos: las Formas y los entes matemáticos, como números y figuras. Esto da lugar a dos tipos de conocimiento: el dialéctico, que consiste en la comprensión intelectual de las Formas, y el matemático, que usa el razonamiento discursivo. La superioridad de la dialéctica estriba en que demuestra todos sus principios, mientras que las matemáticas se fundan en axiomas indemostrables. Para Platón, los entes matemáticos juegan el papel de intermediarios entre las Formas inteligibles y los seres naturales.

De modo consecuente, Platón propone en República que los jóvenes destinados a futuros gobernantes de la polis ideal estudien, entre los 20 y los 30 años, las cinco ciencias matemáticas, que en orden creciente de complejidad son: aritmética, geometría, estereometría, astronomía y armonía. Luego, para completar sus estudios, habrán de estudiar dialéctica cinco años. Según Isócrates, los platónicos usaban las matemáticas para entrenarse en el conocimiento abstracto y en la técnica deductiva. Todas esas ciencias admiten un uso teórico –que Platón considera superior– y un uso práctico, por su utilidad para el comercio, el arte de la guerra, la navegación, la medicina, etc. En su afán de separar las matemáticas ideales de las matemáticas empíricas Platón se permitirá criticar a los grandes matemáticos de su tiempo: a Arquitas por usar las matemáticas para la mecánica y a Eudoxo por no limitarse a hacer una astronomía puramente matemática.

En escritos posteriores Platón, cada vez más pitagórico, irá diluyendo la separación entre Formas y entes matemáticos, pues usará cada vez más conceptos matemáticos para conseguir su objetivo fundamental: la jerarquización de los principios de todo lo que existe, mediante el método de generalización y división. Veamos algunos ejemplos en sus diálogos de vejez. Mientras que en República la Forma suprema es el Bien, en Las Leyes, su obra postrera, será la Unidad. Cuando presenta su cosmología en el Timeo, adjudica a las partículas que componen los cuatro elementos físicos –tierra, agua, aire y fuego– formas de poliedros regulares –hexaedro, icosaedro, octaedro y tetraedro. Ahí mismo distingue tres géneros de ser: las Formas eternas inmutables, el Espacio y los seres naturales. Asimismo en El Sofista presenta como géneros supremos cinco: el ser, el reposo y el movimiento, lo igual y lo desigual. En el Teeteto se afirma que tras percibir las sensaciones el alma compara y distingue lo semejante y lo diferente: esa reflexión constituye la ciencia. Convencido de que las matemáticas expresan la necesidad de la verdad, Platón llegará a decir en Las Leyes que “los dioses no se resisten ni luchan contra las matemáticas”.

Al final de su vida, Platón consideraba que había unas pocas Formas de números: desde la Diada hasta la Década. La Forma o Idea Diada, por ejemplo, era el arquetipo de todo lo dual, no sólo del numero dos, sino también de lo doble y de la dicotomía. En el Filebo dirá que el Número es el principio intermedio entre lo Uno y lo Ilimitado. En algunos escritos Platón recoge la doctrina pitagórica de lo par y lo impar como elementos constituyentes de los números y explicará la generación de los números –y de las magnitudes– en función de dos principios: la Unidad y la Diada indeterminada, también llamada Diada de lo Grande y lo Pequeño. Lo Pequeño hace referencia al problema de la divisibilidad continua y las unidades mínimas y lo Grande al límite del cosmos y al número que numeraría todas las cosas. Parece ser que algunos miembros de la Academia platónica consideraban que los números se generaban a partir de dos principios: la Unidad y lo Desigual; queda claro que si se ve lo Desigual como lo opuesto a la Unidad era porque esta representaba esencialmente lo Igual, lo que hace a la cosa igual a sí misma y le da su identidad. Hay indicios de que en sus últimos años pudo enseñar una teoría de los números ideales, que no llegó a escribir, donde asociaba las Formas fundamentales a los números de la Década.

Actividades

1. Exponer el llamado “Teorema de Tales” y averiguar algún otro teorema que se le atribuya como autor.
2. Exponer el “Teorema de Pitágoras” y averiguar qué civilización anterior a la griega ya conocía el teorema y lo usaba.
3. Averiguar el origen matemático de los símbolos pitagóricos: la tetractys y la pentalfa.
4. Investigar qué libros de los “Elementos” de Euclides recogen directamente los conocimientos matemáticos elaborados por los pitagóricos.
5. Averiguar cuáles eran para Platón las figuras más perfectas en dos y en tres dimensiones. Explicar la razón.
6. Explicar en qué consiste la teoría de las esferas homocéntricas de Eudoxo.
7. Indagar en qué diálogos platón hace polemizar a Sócrates con reconocidos sofistas
8. Averiguar sobre qué temas escribieron los pitagóricos Filolao de Crotona y Arquitas de Tarento
9. Averiguar los nombres de al menos cuatro astrónomos griegos, anteriores o posteriores a Platón, que defendieron que la Tierra giraba alrededor del Sol.
10. Exponer las fases históricas de la existencia de la Academia de Platón desde su fundación hasta su clausura por el emperador bizantino Justiniano.

Para saber más

• Platón y la Academia de Atenas, Pedro González Urbaneja, Ed. Nivola.
• La geometría en la cultura griega, José Luis Prieto, Biblioteca digital de Fundoro, (PDF).
• Tales: El comienzo de la geometría racional, Biblioteca digital de Fundoro, (PDF).
• La geometría pitagórica, Sergio Toledo, Biblioteca digital de Fundoro,(PDF).
• El continuo y el infinito en la matemática griega,José Montesinos, Biblioteca digital de Fundoro, (PDF).
• Platón: Matemática y Dialéctica, Alberto Relancio, Biblioteca digital de Fundoro, (PDF).
• Eudoxo y la matemática, Carlos Mederos, Biblioteca digital de Fundoro, (PDF).
• Matemáticas y filosofía en Grecia: Intercambios, Sergio Toledo, Biblioteca digital de Fundoro, (PDF).