Las Matemáticas en la República de Platón

Los objetivos de República

"La República", de Platón. Ejemplar de 1713. Una escuela en la antigua Grecia 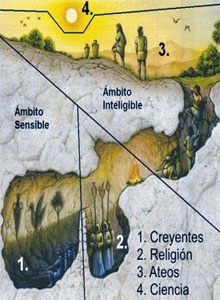Representación del mito de la caverna 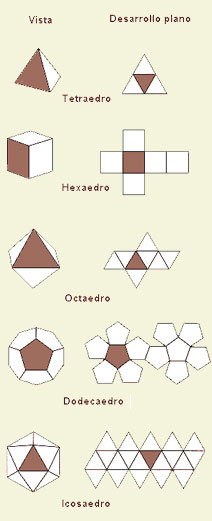Poliedros regulares y su desarrollo en el plano

República es el diálogo más famoso de Platón, una obra en diez capítulos redactada a lo largo de dos décadas que tiene a Sócrates como personaje principal. Su objetivo es investigar qué es la justicia y, en consecuencia, proponer un modelo de Estado y un sistema educativo que propicien una sociedad justa y feliz. En el capítulo V introduce la existencia de las Formas o Ideas, arquetipos presentes en las cosas sensibles. Esta noción platónica de “idea” muestra ya la influencia de las matemáticas en su obra. En efecto, tanto su maestro Sócrates como él mismo tomaron de los pitagóricos la convicción de que el universo estaba regido por principios matemáticos. Lo que hace Platón es extender esa posición y sostener que hay un conjunto de principios que dirigen no sólo la actividad de las cosas corpóreas, sino la propia existencia de las cosas y, sobre todo, la existencia y la actividad de los seres vivos. Esos principios -las Formas o Ideas- son externos al mundo sensible, puesto que son incorpóreos, como los principios matemáticos. Platón distingue entre la opinión, conocimiento que se basa sólo en las percepciones sensibles, propio del hombre corriente, y la ciencia, conocimiento que razona con Ideas y es propio de los filósofos. Son estos, en cuanto amantes de la verdad, necesaria para hacer justicia, quienes deber gobernar el Estado. Deben poseer virtudes como memoria, inteligencia, valentía, generosidad, magnanimidad y moderación. Platón considera una tarea fundamental del Estado proporcionar la educación adecuada a quienes han de ser sus futuros regidores, para que una vez lleguen al gobierno sean capaces de encaminarlo hacia la perfección, superando los males y corrupciones del presente. Esa tarea debe orientarse hacia el conocimiento supremo, el de la Idea del Bien, que es la causa de la existencia y consistencia de las cosas sensibles, y por tanto, de la posibilidad de alcanzar la verdad científica sobre ellas.

Los tipos de Conocimiento y las Matemáticas

Al final del capítulo VI, para señalar las relaciones entre los cuatro tipos de conocimiento que va a distinguir, Platón usa la metáfora de una recta dividida en dos segmentos según una cierta proporción, división que simboliza la que efectúa entre conocimiento sensible y conocimiento inteligible, o sea, entre opinión y ciencia. A su vez cada uno de esos dos segmentos se divide mediante la misma proporción anterior, resultando así cuatro segmentos. La opinión queda dividida en un grado inferior, el conocimiento por conjetura, y un grado superior, el conocimiento por creencia. La ciencia queda dividida en un grado inferior, razonamiento argumentativo, y un grado superior, la comprensión intelectual. La distinción entre creer y conjeturar se basa en que tengamos o no un conocimiento directo de las cosas sensibles. La creencia se apoya en las percepciones actuales de nuestros sentidos, mientras que las conjeturas se basan en las percepciones pasadas, conservadas como imágenes en la memoria. De modo que las creencias tienen mayor capacidad de convicción que las conjeturas y mayor probabilidad de certeza. La distinción entre razonar e inteligir se basa en el modo de operar con los entes ideales. Para explicarla Platón echa mano de la diferencia entre los dos métodos inversos que usan los matemáticos para resolver problemas. El de síntesis consiste en partir de unos principios o axiomas, cuya verdad se da por supuesta y evidente, para alcanzar una conclusión: un teorema. El método de análisis consiste en dar por supuesta la solución de un problema para retroceder hacia los principios que la justifican. Pues bien, Platón afirma que las ciencias actúan de modo sintético, partiendo de principios que no demuestran, sino que dan como verdaderos por evidentes, para alcanzar conclusiones verdaderas mediante demostración. Por el contrario, la dialéctica, que es el conocimiento mediante comprensión intelectual de las Ideas, actúa de modo analítico, retrocediendo desde las ideas simples hasta la idea suprema: la idea de Bien. La superioridad de la dialéctica sobre las ciencias matemáticas consiste en que aquella demuestra su primer principio, que es a la vez el origen -en cuanto causa- y el fin -en cuanto resultado- de todos sus razonamientos; de ese modo no deja nada sin demostrar. Para explicar el funcionamiento del conocimiento dialéctico Platón usa otra analogía matemática: del mismo modo que los matemáticos cuando dibujan sus números y figuras no las consideran reales, sino meras imágenes de los entes ideales a los que se refieren, los filósofos tienen que razonar con las Ideas pensando en cómo son estas por sí mismas, no pensando en las copias de ellas que constituyen las cosas del mundo sensible. Así se recalca que la dialéctica sólo puede ser un pensamiento lógico, no empírico.

La Educación Matemática

Platón reconoce la dificultad del aprendizaje de las matemáticas y de la dialéctica mediante el mito de la caverna. Conocer solamente las cosas sensibles es condenarse al mundo de las sombras, a la mera opinión. Sólo quien se libera de las cadenas del conocimiento sensible y dirige su mente hacia los entes matemáticos y las ideas se halla en condiciones del alcanzar el conocimiento verdadero sobre la realidad. Así pues, Platón va a plantear que el Estado debe crear un sistema educativo para los futuros gobernantes basado en el estudio de las matemáticas y de la dialéctica. Esa educación debe empezar en la infancia para fortalecer el carácter frente a las tentaciones del mundo sensible que apartan de la virtud, como el placer, la riqueza y la ambición. El orden del mundo debe ser el modelo a imitar en la vida. Los años de infancia y adolescencia deben dedicarse al estudio de las artes, como la música y la poesía, y luego, durante dos o tres años, al cultivo del cuerpo mediante la gimnasia, necesaria para la salud y para la guerra. Al llegar a los 20 años, se seleccionará a aquellos alumnos que posean gran sagacidad y facilidad de aprendizaje, al mismo tiempo que un carácter con las disposiciones apropiadas, tales como serenidad, constancia, fortaleza, interés por la verdad, amor al trabajo y a la vida ordenada. La primera disciplina que Platón propone para su estudio es la aritmética, ciencia de los números y el cálculo que, aparte de su utilidad para el comercio y la estrategia militar, ejercita la mente elevándola hacia el mundo de los entes ideales. La segunda disciplina a estudiar debe ser la geometría, ciencia de las figuras planas y de las proporciones que, aparte de su utilidad práctica para el arte de la guerra, también eleva la mente hacia la contemplación del mundo inteligible. La tercera ha de ser la estereometría, es decir, la geometría de las figuras de tres dimensiones, que Platón reconoce que está todavía en sus comienzos, gracias a los matemáticos de la Academia, como Teeteto, y otros. La cuarta es la astronomía que, yendo más allá de la mera observación de los astros por su utilidad para fijar el calendario agrícola y religioso, debe estudiar el orden matemático de sus movimientos. Se cree que fue el propio Platón quien encargó al matemático Eudoxo de Cnido, durante su estancia en la Academia, la elaboración del primer modelo matemático de los movimientos celestes, que se conoce como “teoría de las esferas homocéntricas”. La quinta disciplina es la armonía, que consiste en el estudio de las proporciones matemáticas de los sonidos musicales. También aquí se trata de avanzar desde la mera ejecución y audición de la música hasta los principios ideales que la rigen. Estas cinco disciplinas constituyen un camino de ascesis y ascenso. De ascesis porque requieren un ejercicio esforzado, mediante el cual en cada una de ellas se aprende a pasar desde lo sensible hacia lo inteligible, es decir, desde las cosas contadas, hacia los números ideales, desde las figuras trazadas hacia las figuras ideales, desde los sólidos diseñados hacia los sólidos ideales, desde las trayectorias astrales hacia los principios matemáticos que rigen los cielos, desde los sonidos escuchados hacia los principios que rigen los sonidos armónicos. Y a la vez es un camino ascendente, porque cada ciencia es más compleja y difícil que la anterior, entre otras cosas porque cada una de esas ciencias integra procedimientos, conceptos y resultados de las anteriores. Platón propone que los candidatos a gobernantes del Estado estudien esas disciplinas matemáticas durante una década, a partir de los 20 años. En ese momento se volverá a seleccionar a los que mejores capacidades hayan demostrado y se les instruirá durante cinco años en la dialéctica, es decir, en la filosofía que indaga sobre el mundo de las Ideas, donde el Bien es la idea primordial. Es la última fase de la educación, antes de que empiecen a ocupar cargos políticos en el Estado.

Actividades

1. Explicar qué semejanza hay entre los principios matemáticos pitagóricos y las Ideas platónicas.
2. Exponer qué diferencia principal establece Platón entre las matemáticas y la dialéctica.
3. Explicar qué quiere expresar Platón con la metáfora de la línea recta dividida en partes proporcionales.
4. Exponer un ejemplo de cada uno de los cuatro tipos de conocimiento que distingue Platón.
5. Argumentar por qué el Estado debe encargarse de la educación.
6. Averiguar de qué forma queda simbolizado el conocimiento matemático en el mito platónico de la caverna.
7. Averiguar y exponer brevemente en qué consiste la teoría de las esferas homocéntricas de Eudoxo de Cnido.
8. Indagar y resumir las teorías de los pitagóricos sobre la armonía musical.
9. Razonar por que Platón exige a los futuros gobernantes del Estado las disposiciones de carácter citadas en el texto.
10. Exponer por qué la práctica de las ciencias matemáticas constituye un camino ascético.

Para saber más

• Platón y la Academia de Atenas, Pedro González Urbaneja, Ed. Nivola.
• La geometría en la cultura griega, José Luis Prieto, Biblioteca digital de Fundoro, (PDF).
• Platón: Matemática y Dialéctica, Alberto Relancio, Biblioteca digital de Fundoro, (PDF).
• Eudoxo y la matemática, Carlos Mederos, Biblioteca digital de Fundoro, (PDF).
• Un libro sobre Platón, Antonio Tovar, Ed. Círculo de Lectores.
• Los mitos platónicos, Geneviève Droz, Ed. Labor.