Zenón de Elea cotra el Pitagorismo
 Zenón de Elea (s. V. a.n.e)
Zenón de Elea (s. V. a.n.e)
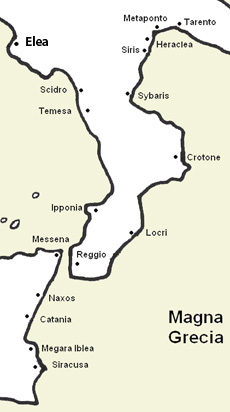 Mapa de las colonias griegas al sur de la península Itálica
Mapa de las colonias griegas al sur de la península Itálica
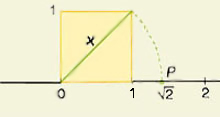
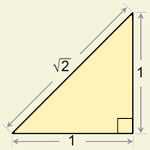 Para un cuadrado de lado 1 la diagonal resulta √2, un número irracional
Para un cuadrado de lado 1 la diagonal resulta √2, un número irracional
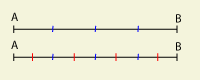 El segmento A-B no varía de tamaño al añadir puntos intermedios
El segmento A-B no varía de tamaño al añadir puntos intermedios
Zenón vivió en Elea entre el 480 y el 420 a.n.e., aproximadamente. En esa ciudad de la Magna Grecia, cercana a la actual Nápoles, fue discípulo de Parménides y adoptó su filosofía, que rechazaba las doctrinas de la escuela pitagórica, que se había fundado y desarrollado más al sur, en ciudades de Sicilia. Los fragmentos conservados de la obra de Zenón se conocen como “aporías” contra la pluralidad y el movimiento. Se llaman así porque se basan en la idea de que lo ilimitado “apeiron” no es concebible y no puede existir.
Aporías contra la pluralidad
Los primeros pitagóricos consideraban que las cosas estaban compuestas de unidades iguales. Pensaban estas unidades como si fueran aritméticas, geométricas y físicas a la vez, es decir, como si fueran números, puntos y átomos. Tuvieron que abandonar esta doctrina por dos motivos. Primero, porque los propios matemáticos pitagóricos descubrieron que hay magnitudes irracionales, que son inconmensurables entre sí, como el lado y la diagonal del cuadrado; o sea, dado un lado que tenga un determinado número de unidades no es posible expresar el valor de la diagonal mediante otro número de unidades, ni viceversa. Segundo, porque los argumentos de Zenón contra esa doctrina les obligaron a sustituirla por el naciente atomismo físico. Expondremos las aporías tal como se han conservado en Simplicio, un historiador de la filosofía del siglo VI d.n.e.:
“Si existe una pluralidad es necesario que las cosas sean tantas cuantas son, ni más ni menos. Y si son tantas cuantas son deben ser limitadas.”
Esto significa que si cualquier cuerpo físico está formado por unidades, la cantidad de estas es un número concreto y limitado, no unas veces más y otras veces menos. Y continúa el argumento:
“Si existe una pluralidad las cosas existentes son infinitas, pues siempre hay otra cosa entre ellas y, a su vez, otras más entre esas otras. Y por tanto las cosas que hay son ilimitadas.”
Aquí Zenón está tratando las unidades pitagóricas como si fueran geométricos. En tal caso, igual que en una línea siempre hay puntos entre cualesquiera dos puntos determinados, entre cualesquiera dos unidades que forman parte de un cuerpo físico siempre habría otras unidades, y así indefinidamente, por lo que su cantidad de unidades tendría que ser ilimitada. Si Zenón puede razonar así es porque se está aprovechando de la confusión de los primeros pitagóricos sobre su concepto de unidades, por pensarlas simultáneamente como numerables y como puntos yuxtapuestos que dan dimensión a los cuerpos físicos.
Si juntamos los dos fragmentos anteriores veremos que lo que pretende Zenón es afirmar que la doctrina de que las cosas están compuestas de unidades no es racional, porque nos conduce a pensar que los cuerpos físicos están compuestos de un número de unidad que resulta ser, a la vez, limitado e ilimitado. Puesto que esto es contradictorio se deduce que la hipótesis de partida, la composición de unidades, es falsa.
Otro de los argumentos de Zenón contra la pluralidad, recogido por Simplicio, ataca otro aspecto de la doctrina pitagórica de las unidades. Empieza así:
“Si existe una pluralidad las cosas serán también grandes y pequeñas; tan grandes como para poder ser infinitas en tamaño y tan pequeñas como para no tener tamaño alguno.”
Lo que dice Zenón es que si las cosas están formadas por unidades podrían tener un tamaño infinitamente grande o infinitamente pequeño, dependiendo de si consideramos que esas unidades tienen tamaño o no.
“Si lo que hay no tuviera tamaño ni siquiera sería. Pues si se le añade a cualquier otra cosa no la hace más grande, ya que al no tener tamaño alguno no puede, al añadirse, aumentar su tamaño. Y por tanto lo añadido no es nada”
O sea, que si las unidades no tienen tamaño no aumentan el tamaño de las cosas al agregarse a ellas.
“Del mismo modo, es evidente que ni lo añadido ni lo quitado son nada si la cosa a la que se le quita no se hace más pequeña, y si al añadírselo no aumenta.”
El argumento es simétrico del anterior. Si al quitarle unidades a una cosa tampoco cambia de tamaño eso significa que lo añadido no es nada. En consecuencia, deduce Zenón, si las unidades no tienen tamaño entonces no existen. Y ahora Zenón pasa a la segunda hipótesis: que las unidades sí tengan tamaño.
“Pero si existe es necesario que cualquier cosa tenga un cierto tamaño y espesor y que una parte diste de la otra. Y el mismo razonamiento vale para las demás partes. También esto tendrá un cierto tamaño y habrá una parte siguiente. Y es lo mismo decir esto una vez que irlo afirmando sin fin, pues ninguna parte igual suya será la última ni una parte dejará de tener relación con la otra.”
Para entender este fragmento, menos claro que los anteriores, tenemos que imaginarnos una cosa compuesta por una yuxtaposición de unidades con tamaño, que le dan longitud y espesor. Zenón está diciendo que entre cada unidad y la siguiente hay una cierta distancia, ya que tienen tamaño. Y a continuación aplica un razonamiento de tipo geométrico al conjunto de unidades de que se compone una cosa: las trata como si fueran puntos de un segmento y afirma que entre cualesquiera unidades que tomemos, separadas por cierta distancia, habrá otras unidades intermedias, también separadas por una cierta distancia y que esto ocurre de modo ilimitado. La conclusión de Zenón es que una cosa compuesta por un conjunto ilimitado de unidades con magnitud tendrá un tamaño ilimitado, es decir, sin medida.
Actividades
- Señalar algunas diferencias fundamentales entre números, puntos y átomos.
- Razonar sobre por qué los números se inventaron antes que los puntos y que los átomos.
- Indicar si hay alguna conexión entre la invención del concepto de punto y la invención del concepto de átomo.
- Explicar qué conexión hay entre las aporías contra la pluralidad de Zenón y la doctrina de Parménides sobre lo Uno.
- Exponer cuál es el principal objetivo de Zenón al atacar la idea de que las cosas están formadas por un conjunto de unidades iguales.
- Imaginar argumentos a favor de que las cosas materiales están formadas por unidades indivisibles, o sea, átomos.
- Establecer alguna relación entre las ideas griegas sobre los átomos y las ideas de la Física actual sobre los átomos.
- Explicar que significan las “cantidades inconmensurables o irracionales”.
- Investigar cuál es la aporía que se atribuye a Zenón conocida como la “aporía del grano de mijo”.
- Averiguar datos sobre la vida y obra de Simplicio.
Para saber más
- Los filósofos presocráticos (tomo II). Introducción de Conrado Eggers Lan, Ed. Gredos.
- Los filosofos presocráticos. Kirk, G.S. y Raven J. E., Editorial Gredos.
- Los presocráticos. Miguel Morey, Ed. Montesinos.
- Mitología y filosofía: Los presocráticos. Ángel Capelletti, Ed. Cincel.