Aristóteles y el círculo: el movimiento de las estrellas
Aun más, esta noción circular es necesariamente primaria. Pues lo perfecto es naturalmente anterior a lo imperfecto, y el círculo es algo perfecto. Esto no puede ser dicho de la línea recta
Aristóteles, De Caelo, 269a 19-21
(...) pero indudablemente la idea de la infinitud asumía mayor vigor y carácter de necesidad lógica al ser representada en una forma geométrica que por sí misma hiciese contradictoria e inadmisible la determinación de un límite inicial o final (...) y esta era precisamente el círculo (...), la representación de una especie de círculo como la que hay en el movimiento del cielo y de cada uno de los astros, por la cual llegamos a establecer una serie ordenada de manera tal que retorna nuevamente al principio y lo hace sin cesar y se comporta siempre del mismo modo (...).
R. Mondolfo, El infinito en el pensamiento de la antigüedad c!ásica
 Aristóteles (s. IV a.n.e.)
Aristóteles (s. IV a.n.e.)
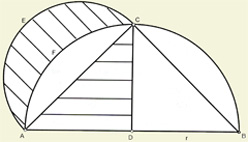 Cuadratura de la primera lúnula
Cuadratura de la primera lúnula
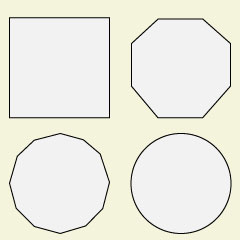 Aproximación geométrica al círculo
Aproximación geométrica al círculo
 Foto del cielo nocturno de larga exposición. Al centro se aprecia la Estrella Polar como un punto fijo.
Foto del cielo nocturno de larga exposición. Al centro se aprecia la Estrella Polar como un punto fijo.
 Aristóteles. "Physicorum libri VIII. Quibus adjecimus omnia illius opera ad naturalem philosophiam spectare..." Lyon, 1580.
Aristóteles. "Physicorum libri VIII. Quibus adjecimus omnia illius opera ad naturalem philosophiam spectare..." Lyon, 1580.

 Páginas del "Timeo" de Platón, traducido al latín, en el siglo V, por el helenista Calcidius.
Páginas del "Timeo" de Platón, traducido al latín, en el siglo V, por el helenista Calcidius.
Muy pronto se haría famoso el problema de la cuadratura del círculo, esto es, la manera de construir, únicamente con regla y compás, un cuadrado de superficie igual a la de un círculo dado. Hipócrates de Quios, contemporáneo de Enópides había cuadrado ciertas lúnulas, figuras de contorno curvo, en principio más complicadas que el círculo, lo que hizo despertar esperanzas de una pronta resolución del problema. Para ello, Hipócrates habría dado el paso, de manera intuitiva, de lo recto a lo curvo, de lo finito a lo infinito, considerando el círculo como “límite” de polígonos de infinitos lados. Antifonte , el sofista, contemporáneo de los anteriores, “cuadró” el círculo simplemente negando que fuese necesario el paso de lo finito a lo infinito: en su geometría empírica (como de carpinteros), el círculo coincidiría con un polígono inscrito de un número suficientemente grande de lados y el problema estaría resuelto ya que era bien sabido cómo cuadrar un polígono. Esta “cuadratura” levantó las iras de Aristóteles, muy interesado en el tema, que no se dignó siquiera refutarla, por no atenerse a las condiciones del problema. Sin embargo la idea de Antifonte es fructífera, si de lo que se trata es de “aproximarse a la circularidad”. Así lo entendió Arquímedes para conseguir una excelente aproximación del número π.
Esta continuada tensión histórica entre lo recto y lo circular tuvo su reflejo en la legitimación teórica del conocimiento astronómico empírico. El uniforme movimiento de las estrellas, contemplado y estudiado por los seres humanos, había conferido al movimiento circular los calificativos de natural, continuo, simple, perfecto, eterno, espacialmente limitado, contraponiéndolo al movimiento rectilíneo que en un Cosmos finito y ordenado estaba obligado necesariamente a terminarse, a tener un final.
Será Aristóteles quien en el libro VIII de su Física determine la excelencia del movimiento circular, su primacía en la jerarquía de los movimientos:
“Clearly circular motion is the primary kind of locomotion. For all locomotion is either circular, rectilinear, or mixed. Now the simple kinds must be prior to the mixed. And the circular kind is prior to the rectilinear; for (1) it is simpler and more perfect. For it is impossible to move along an infinite straight line (since there is not such thing, and if there were it could not be traversed); and motion along a finite one, if it turn back, is really two motions, while if it does not it is imperfect and comes to an end. But the perfect is prior to the imperfect, the imperishable to the perishable, by nature, in definition, and in time.(2) A motion that can be eternal is prior to one that cannot; now circular motion can, and no other locomotion or indeed change can, since it must be interrupted by rest”.
Aristotle’s Physics, W. D. Ross. VIII 265ª 13-24.
No solo Aristóteles había hablado de la superioridad de lo circular. También su maestro, Platón, había establecido la prioridad como indica aquí el historiador de la Ciencia E. J. Dijksterhuis :
“The axiom of the uniformity and circularity of the motions of the heavenly bodies, which Plato had framed on mathematical and religious grounds, had been supported by Aristotle with physical arguments and made an essential part of his world-system; enunciated unanimously by two such authoritative thinkers, it was bound to appear beyond all doubt. Nor did astronomers venture to deviate from this view before the beginning of the seventeenth century, an even then they only undertook this most revolutionary of all changes in the ancient world-picture from sheer necessity.”
The Mechanization of the World Picture
Pero Aristóteles no sólo estableció la superioridad del movimiento circular. En su libro sobre la Física VII, 4, expone lo que parece ser una prohibición de "comparar" los movimientos circular y rectilíneo:
"The question may be asked whether all movements are comparable in respect of speed (...) The fact remains that if the motions are comparable, there will be a straight line equal to a circle. But the lines are not comparable; so neither are the motions"
¿En qué sentido afirma Aristóteles que la recta y el círculo no son comparables? No puede ser en el sentido bien preciso de inconmensurables, porque si bien él sabe -porque ya se había demostrado- que la diagonal y el lado de un cuadrado son inconmensurables, es sólo en el siglo XVIII que Lambert demuestra, por primera vez, que el número π es irracional o lo que es equivalente que la circunferencia y su radio son inconmensurables. Todo lo más, Aristóteles puede "sospechar" esa inconmensurabilidad.
Un poco más adelante en ese texto se dice:
"... things that are not called by the same name in the same sense are not comparable"... May we not say then that "fast" does not mean the same thing when applied to circular and rectilinear motion?
¿Sugiere esta idea ya la concepción de la velocidad como una magnitud vectorial, que solo encontraremos después por primera vez en Newton?
Ross en la Introducción a su celebrada edición de la Física, después de referirse a las deficiencias de la dinámica aristotélica, señala que en el libro VII se trataría al movimiento circular local como el resultante de dos movimientos rectilíneos simples:
...Hay cuatro formas de desplazamiento de una cosa por otra: tracción, empuje, transporte y rotación... Y de esos cuatro, también el transporte y la rotación se reducen a la tracción y el empuje...En cuanto a la rotación, es un compuesto de tracción y empuje, porque lo que hace rotar tiene que tirar de una parte de la cosa y empujar la otra parte, ya que a una parte la aleja de sí y a otra la atrae hacia sí
Añade Ross que si Aristóteles hubiese extendido este análisis al movimiento circular de las esferas celestes, se habría situado en la vía correcta, la que llevó a Newton a su explicación del Sistema del Mundo.
Pero en realidad, la autoridad aristotélica impondrá a la comunidad sabia el movimiento circular como el movimiento natural durante los siguientes dos mil años. Y esto no sólo era válido para la física de los cielos sino también lo será para la terrestre, como se demostraba en la Mecánica, en la que el círculo era la base de la balanza, y ésta de la palanca, y ésta a su vez de todas las máquinas simples: las Quaestiones Mechanicae, escritas cien años después de Aristóteles por seguidores de éste, exaltarán las maravillas del círculo:
... porque no es nada extraño que una maravilla menor sea causada por una mayor, y es una muy grande maravilla que los contrarios estén juntos, y el círculo está hecho de contrarios: ...movimiento y reposo ... cóncavo y convexo...se mueve en direcciones contrarias al mismo tiempo
Este libro, recuperado en el Renacimiento italiano tendrá una gran influencia en la mecánica italiana del siglo XVI y en particular en Galileo.
Actividades
- Traduce cuidadosamente los textos que están en inglés.
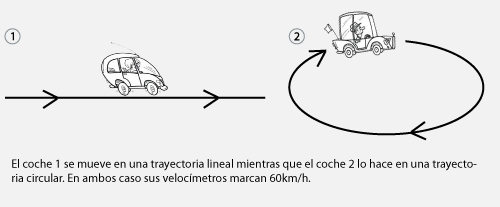
- Comenta con tu profesor el concepto actual de velocidad como una magnitud vectorial. ¿Por qué la velocidad que marca el velocímetro de un automóvil no distingue entre un trayecto rectilíneo y uno circular? ¿ Por qué en la física moderna sí se distingue?

- Busca en el Timeo de Platón el texto en el que el Demiurgo forja el alma del Mundo con rectas y círculos. Busca y copia entre los cinco postulados de los Elementos de Euclides aquellos que se refieren a las construcciones con rectas y círculos.
Para saber más
- Montesinos Sirera, José: "Historia de las Matemáticas en la Enseñanza Secundaria". Editorial Síntesis: Madrid, 2000.
- Marachia, Silvio: "Aristóteles e la matemática", Historia de la geometría griega. Fundación Canaria Orotava de Historia de la Ciencia: La Orotava, 1992.