Infinito, Esferas y Cosmología: Eudoxo de Cnido

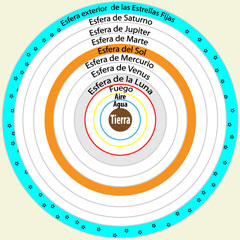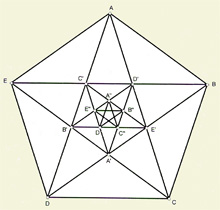Pitágoras de Samos Aquíles y la tortuga Cosmos aristotélico con las ocho esferas rodeando a la Tierra Eudoxo de Cnido Pentágono regular Recreación de la Biblioteca de Alejandría Primera traducción al castellano de Rodrigo Zamorano, 1576

A partir del siglo VII a.C. tiene lugar progresivamente en Grecia lo que se conoce como "paso del mito al logos", es decir, la sustitución del mito por la razón en la explicación de la realidad. Como primer paso, los pitagóricos, seguidores de la secta matemático-religiosa liderada por Pitágoras, dan una interpretación mítico-racional de la realidad, en la que las matemáticas eran un instrumento para comprender el comportamiento de la Naturaleza. Ellos pensaban que en el Universo a todas las cosas se les podía asignar número y por lo tanto los fenómenos naturales eran entendidos como relaciones entre números. Estas ideas aparecen resumidas en el lema de la escuela: "Todo es armonía y número en el Universo". Poco a poco se va configurando la visión griega del Universo como un Cosmos, algo que estaba armoniosamente organizado y dotado de una simetría, es decir, como algo bien proporcionado, en el que las partes estarían acordes con el todo. Esta forma de entender el Universo produce una serie de consecuencias en el desarrollo de las Matemáticas. El hombre contempla la naturaleza y estudia las relaciones idealizadas entre las figuras planas y sólidas que va observando. Es una geometría de un espacio finito, de pequeñas distancias, en donde el paradigma es el cuerpo humano; y así, el arte griego por excelencia es la escultura.

Pero en algún momento de la primera mitad del siglo V a.C. tiene lugar en Grecia un descubrimiento demoledor para la aritmo-geometría pitagórica: la existencia de magnitudes inconmensurables. La diagonal y el lado de cualquier cuadrado son inconmensurables, esto es, no existe un segmento (por pequeño que sea) que pueda ser contenido un número exacto de veces tanto en el lado como en la diagonal de un cuadrado, ya que si lo intentamos buscar utilizando el procedimiento geométrico correspondiente, caemos en un proceso sin fin (infinito). Los números naturales no bastaban ya para cuantificar y medir todos los segmentos de recta que producen las construcciones geométricas. El gran matemático Eudoxo de Cnido, alumno de Platón, desarrollará toda una complicada teoría de las proporciones (que constituirá posteriormente el Libro V de Los Elementos de Euclides) y que permitirá comparar magnitudes de cualquier tipo.

Las consideraciones sobre la infinitud han supuesto desde un principio un gran problema para la razón, y la Historia de las Matemáticas y de la Filosofía es un continuo sortear las dificultades que los procesos infinitos llevan consigo. Ya desde el siglo V a.C., el filósofo griego Zenón de Elea puso a la razón en un callejón sin salida al enfrentarla con ciertos procesos infinitos, dando lugar a sus conocidas paradojas, siendo la más conocida la de Aquiles y la tortuga, en la que Aquiles, el corredor más veloz de Grecia, nunca alcanzaría a la tortuga si le dejase una cierta ventaja inicial. Aristóteles, el gran sabio de la Antigüedad, recopilador de todo el saber de su época, veta el concepto de infinito como algo extraño, imperfecto, indeterminado, innombrable. Aristóteles ha comprobado el peligro que representaba para la Razón algo que la misma Razón había inventado: "pero la consideración del infinito conlleva una dificultad (aporía), pues tanto al afirmar que no existe resultan muchos imposibles, como al afirmar que existe" (Física 203 b 30-32).

Uno de los legados más importantes que los griegos dejaron a la posteridad fue el de sus ideas y conocimientos en Astronomía. Fue Eudoxo el primero en concebir un modelo matemático del Universo sirviéndose de la figura geométrica más perfecta: la esfera. La estructura del mundo estaría formada por una serie de esferas concéntricas, en el centro de las cuales estaría la Tierra y en ella el hombre, observador paciente, que sin otro instrumento óptico que el de sus ojos, iba anotando datos y comportamientos de los objetos celestes. El modelo se fue perfeccionando con las aportaciones de Calipo, Aristóteles, Aristarco, Hiparco y finalmente Ptolomeo, ya en el siglo II d.C., y el objetivo era el de "salvar las apariencias", es decir, dar cuenta, con explicaciones - que cada vez resultaban más complicadas- de las anomalías que eran observadas: el extraño movimiento de los planetas, las diferencias en la intensidad del brillo de éstos, etc. El modelo final, denominado aristotélico-ptolemaico "funcionaría" y explicaría mal que bien nuestras elucubraciones cósmicas hasta la época de Galileo. Aristóteles, con su enorme saber enciclopédico era la autoridad que refrendaba la explicación física del modelo.

La física y la cosmología de Aristóteles están construidas alrededor de dos ideas principales: la teoría de los cuatro elementos y la teoría de los lugares naturales. Los cuatro elementos serían la tierra, el agua, el aire y el fuego, y el lugar que ocupan en el mundo está en función de una intrínseca nobleza: la tierra, que es el elemento más vil está en el lugar más bajo, en el centro, sobre ella está el agua, después el aire y a continuación el elemento más noble que es el fuego. Todo esto constituiría el mundo sublunar, que es corruptible; y luego vendría la esfera de la Luna, a partir de la cual todo estaría constituido por la quintaesencia, el éter, que es perfecto, eterno e incorruptible. Después vendrían las esferas, en que estarían encastrados el Sol y los Planetas; y finalmente, la octava esfera, la esfera de las estrellas fijas, que sería el límite del Universo. El movimiento se transmite desde la última esfera hasta las más internas haciendo presión sobre el éter. La rotación del cielo de la Luna y su roce con el fuego y el aire de abajo provocaría la mezcla y el torbellino de los cuatro elementos, base de la generación y corrupción del mundo sublunar.

En el año 340 a.C. Aristóteles tuvo un alumno muy especial, el joven de quince años Alejandro, hijo del rey Filipo de Macedonia, cuyas proezas guerreras asombrarían al mundo. Conquista el Oriente y llega hasta la India. Alejandro Magno murió joven y fue enterrado en Alejandría, la ciudad que él mismo había fundado al oeste de la desembocadura del Nilo. Ptolomeo, general de Alejandro, y sus descendientes van a hacer de Alejandría un emporio económico y comercial, puerto de paso obligado entre Oriente y Occidente, lugar de encuentro de todos los credos y culturas. Poco a poco esta ciudad se hizo la capital cultural del mundo helenizado. Allí se creará un Instituto-Museo dedicado al estudio y enseñanza de la ciencia de aquel tiempo, y una famosa Biblioteca que llegaría a tener más de quinientos mil volúmenes. Y allí floreció una escuela de matemáticos y astrónomos que forman una buena parte de la llamada ciencia helenística. Euclides, Aristarco, Eratóstenes, Arquímedes y Apolonio son los principales personajes que cerrarían el brillante y en cierto modo, extraño periodo (siglos V, IV y III a.C. en Grecia), en que la matemática teórica, estrechamente ligada a la Filosofía, se desarrolló "per se", como un bello juego intelectual - según Aristóteles-, y para su maestro Platón como la necesaria preparación del ser humano para acceder a la Dialéctica, el más alto estadio de la contemplación y comprensión de la Realidad.

Euclides, alrededor del año 300 a.C. escribió el libro de matemáticas que más veces se ha impreso a lo largo de la historia: Los Elementos, ordenada y magnífica recopilación de toda la matemática pre-euclídea, libro que está animado platónicamente pero que es de formulación lógica aristotélica. Su organización, ingenio y claridad, inspiraron el tratamiento axiomático-deductivo no sólo de otras ramas de las matemáticas sino de todas las demás ciencias.

Actividades

1. Aunque el ejemplo más sencillo con el que se ilustra el concepto de inconmensurabilidad es el de la diagonal y el lado del cuadrado, parece ser que los antiguos griegos hicieron el descubrimiento de la existencia de magnitudes inconmensurables con la diagonal y el lado de un pentágono regular. Busca en Internet o en la bibliografía asociada a este texto una demostración de ello.
2. Mediante una simple comparación entre dos triángulos semejantes, Eratóstenes consiguió medir el radio de la Tierra con una aproximación aceptable. Busca en Internet una explicación del proceso que le condujo a ello.
3. Para Aristóteles, las Matemáticas eran una bella construcción intelectual que le servía para poner ejemplos de la Lógica, que él formalizó, pero en ningún caso esa disciplina -pensaba él- podía servir para desentrañar los sacretos de la naturaleza. Sin embargo, para su maestro Platón la Matemática era la herramienta necesaria para comprender los fenómenos naturales. Reflexiona sobre esta disidencia y sobre las consecuencias que tuvo en los siguientes dos mil quinientos años...

Para saber más

• Montesinos Sirera, José: "Tales: el comienzo de la geometría racional", Historia de la Geometría griega. Fundación Canaria Orotava de Historia de la Ciencia: La Orotava, 1992. (Arcchivo PDF)
• Montesinos Sirera, José: "El continuo y el infinito en la matemática griega", Historia de la Geometría griega. Fundación Canaria Orotava de Historia de la Ciencia: La Orotava, 1992. (Arcchivo PDF)
• Mederos Martín, Carlos: "Eudoxo y la Matemática", Ciencia y cultura en la Grecia Antigua, Clásica y Helenística.Fundación Canaria Orotava de Historia de la Ciencia: La Orotava, 1992. (Arcchivo PDF)