La aplicación de los conocimientos científicos va a acabar encontrando en los numerosos inventos que se desarrollan durante el período que historiamos un campo abonado, pero quizás sea en el ámbito de las nuevas fuentes de energía –cuyo icono más emblemático es la máquina de vapor– donde esta aplicación acabará resultando más evidente y de mayor impacto. Betancourt, a quien se debe, tras su primera estancia en Inglaterra, la importación de la misma al Continente, escribirá una Memoria sobre la máquina de vapor de doble efecto en 1789 y será un acérrimo defensor de su uso en múltiples parcelas de la actividad industrial: en el dragado de puertos y ríos, en molinos, en la fabricación de armas, en la acuñación de monedas, etc. Por otra parte, también hará una interesante incursión en el campo de la, aún por construir, termodinámica teórica en su Memoria sobre la fuerza expansiva del vapor de agua de 1790.
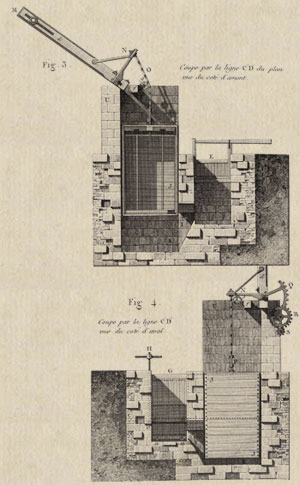 Una buena muestra de ese maridaje entre ciencia teórica y aplicación práctica, que, como hemos señalado con anterioridad, acabará caracterizando la época, la encontramos, por ejemplo, en la Memoria que Betancourt elabora para justificar el diseño de la esclusa de émbolo buzo y que fue presentada en 1807 al Instituto de Francia. En ella utiliza las matemáticas más avanzadas del momento, el cálculo infinitesimal, para obtener las ecuaciones mediante las que formaliza el funcionamiento dinámico de su sistema mecánico –un dispositivo para hacer trabajar en condiciones óptimas una máquina concreta: la esclusa de émbolo buzo.
Una buena muestra de ese maridaje entre ciencia teórica y aplicación práctica, que, como hemos señalado con anterioridad, acabará caracterizando la época, la encontramos, por ejemplo, en la Memoria que Betancourt elabora para justificar el diseño de la esclusa de émbolo buzo y que fue presentada en 1807 al Instituto de Francia. En ella utiliza las matemáticas más avanzadas del momento, el cálculo infinitesimal, para obtener las ecuaciones mediante las que formaliza el funcionamiento dinámico de su sistema mecánico –un dispositivo para hacer trabajar en condiciones óptimas una máquina concreta: la esclusa de émbolo buzo.
Así se expresa Betancourt en la Memoria: Habiendo alcanzado ese resultado teóricamente, [mediante la aplicación del Principio de D´Alembert], hice construir una gran caja en la que sumergí una segunda, cuya base tenía una superficie que era la mitad de la de la primera. La había llenado previamente de agua a fin de darle el mismo peso específico que el del fluido y, habiéndola suspendido del brazo de la palanca angular, comprobé que todo el sistema se mantenía en el más perfecto de los equilibrios cualquiera que fuera la situación del buzo y del contrapeso; he tenido pues la satisfacción de ver que la experiencia concordaba perfectamente con la teoría.
Ese lenguaje, el cálculo infinitesimal, al que hemos hecho mención es, sin duda alguna, la herramienta más potente con la que ha contado la Física porque está diseñado para atrapar aquello que es esencial en esta última ciencia, lo móvil, lo cambiante. Primero se aplicará a las ciencias mecánicas y más tarde, ya en el último tercio del siglo XIX, al electromagnetismo.
 Será a lo largo del siglo XVIII cuando se establezcan los grandes principios de la dinámica –esa parte del conocimiento físico mediante la que se conectan los movimientos, o con más precisión los cambios de movimiento, con sus causas: las fuerzas –el principio de D´Alembert; el teorema del momento de la cantidad de movimiento; el principio de mínima acción. Será también entonces, cuando se formulen, en la forma en que actualmente las conocemos, las ecuaciones de Newton (sí, la famosa ecuación F = ma) y cuando se escriban las primeras ecuaciones diferenciales de la física matemática que rápidamente se utilizan para establecer las ecuaciones generales de la dinámica del punto, del sólido y de los medios continuos, ecuaciones, estas últimas, que abrirán la posibilidad de iniciar la ciencia de la Hidrodinámica.
Será a lo largo del siglo XVIII cuando se establezcan los grandes principios de la dinámica –esa parte del conocimiento físico mediante la que se conectan los movimientos, o con más precisión los cambios de movimiento, con sus causas: las fuerzas –el principio de D´Alembert; el teorema del momento de la cantidad de movimiento; el principio de mínima acción. Será también entonces, cuando se formulen, en la forma en que actualmente las conocemos, las ecuaciones de Newton (sí, la famosa ecuación F = ma) y cuando se escriban las primeras ecuaciones diferenciales de la física matemática que rápidamente se utilizan para establecer las ecuaciones generales de la dinámica del punto, del sólido y de los medios continuos, ecuaciones, estas últimas, que abrirán la posibilidad de iniciar la ciencia de la Hidrodinámica.
Se articula así el cuerpo teórico de lo que conocemos como Mecánica Clásica o Mecánica Racional que, como había apuntado el mismo Newton: será la ciencia que de manera precisa enuncia y demuestra cómo son los movimientos que resultan de la aplicación de fuerzas arbitrarias, –así se expresa el llamado problema directo (dadas las fuerza determinar cuál es el movimiento resultante)– y cuáles son las fuerzas necesarias para crear movimientos arbitrarios –y así el problema inverso (dados los movimientos determinar las fuerzas).











