La Física de Aristóteles (X). El primer motor

Tratamos aquí los cuatro últimos capítulos del libro octavo y final de la Física, tal como fue editada por Andrónico de Rodas. En el séptimo capítulo se establece la primacía del movimiento local sobre los demás tipos; el octavo lo dedica a demostrar que sólo el movimiento circular puede ser uno, continuo e infinito; en el noveno se fija la primordialidad del movimiento circular y en el décimo se explica que el primer motor no tiene magnitud y las consecuencias que de ello se derivan.

1. La primacía del movimiento local

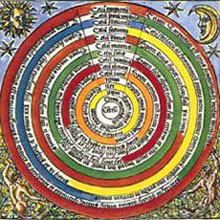"Aristóteles rechazando la cicuta", Giovanni Battista Langetti (1635-1676) Cósmos geocéntico aristotélico Luna girando entorno a la Tierra Animales en un ánfora griega c.a. 550 a.n.e. Reproducción de un reloj griego de agua Detalle de un reloj de arena en una pintura de Lorenzetti, s. XIV Heracles dando muerte a los pájaros de Estínfalo usando una honda, ánfora griega, c.a. 560 a.n.e. Al lanzar una piedra con honda se realiza un movimiento circular Arquero lanzado un proyectil, en ánfora griega, c.a. 540 a.n.e.

Aristóteles se plantea si es posible que haya un movimiento continuo, cómo sería y cual sería el primero de todos los movimientos. Claramente ha de ser de tipo local, pues todo movimiento cuantitativo exige un movimiento cualitativo y este a su vez exige que haya un desplazamiento. Hay otras razones que justifican la primacía del movimiento local. La primera es la superioridad de un movimiento que sea uno y continuo sobre un movimiento múltiple sucesivo, ya que solo el desplazamiento puede ser continuo.

La segunda es la primacía del desplazamiento según el tiempo, pues es el único posible para los seres eternos. Por lo que respecta a las cosas generadas, aunque en su devenir el desplazamiento sea el último de sus movimientos la propia existencia de la cosa exige que haya habido un movimiento previo de desplazamiento: el de su generación por algo que ya es, y de cuya generación a su vez se puede decir lo mismo y así sucesivamente. Pero como no puede haber una cadena infinita hacia atrás de movimientos generadores exclusivamente, pues en ese caso solo habría cosas perecederas, se deduce que el movimiento primero solo puede haber sido un desplazamiento, dado que las alteraciones o aumentos son a su vez posteriores a la generación.

La tercera es la primacía del desplazamiento según el orden de la naturaleza de la sustancia. Toda cosa generada se desarrolla hacia el cumplimiento de su principio. El desplazamiento, siendo el último de los movimientos adquiridos por lo generado es, sin embargo, anterior en el orden de la naturaleza. Así se comprueba al observar que seres animales inferiores no tienen capacidad de desplazamiento, que sí tienen los animales superiores. Además, el desplazamiento es el movimiento que menos aleja de su sustancia a una cosa generada, menos que los cambios de magnitud y las alteraciones. La primacía del desplazamiento es clara en los seres que se mueven por sí mismos.

La respuesta aristotélica al tema de la primacía del movimiento según la continuidad se funda en que, con excepción del desplazamiento, los demás tipos transitan entre opuestos: entre el ser y el no ser, entre cualidades opuestas, entre el más y el menos. Pero tales movimientos no se dan simultáneamente hacia ambos opuestos, de modo que tendrá que haber un tiempo de reposo entre el movimiento en una dirección y el movimiento en dirección contraria; por ejemplo, entre la intensificación y la difuminación de cierto color, o entre el crecimiento y la disminución de un peso. Así pues, esos tipos de movimiento entre opuestos no pueden ser continuos.

2. El movimiento rotatorio es continuo e infinito

Todo movimiento local es rectilíneo, circular o una mezcla de ambos. Un movimiento rectilíneo finito no puede ser continuo porque tiene que volver sobre sí, ya que tiene límites. Siendo un movimiento entre opuestos –sus puntos extremos- no puede ser continuo, ya que en cada límite ha de estar una fracción de tiempo en reposo, antes de cambiar de dirección. Esto es tanto una intuición sensible como una exigencia de la razón. En efecto, si se piensa ese movimiento sin tal tiempo de reposo se cae en la contradicción de que el móvil, cuando está en el punto extremo, tiene a la vez ambas direcciones, está llegando y se está yendo

Para analizar un movimiento hay que considerar tres aspectos: lo que se mueve, su tiempo y su en qué: lugar, forma, afección o magnitud. Aristóteles distingue entre movimiento rotatorio –siempre en la misma dirección- y movimiento circular, en el que el móvil puede invertir su dirección. Tanto en el movimiento rectilíneo como circular el punto de cambio de dirección es doble: fin de una trayectoria y principio de otra, separadas por el tiempo de detención. Todo punto intermedio de la trayectoria es en potencia doble: el móvil puede llegar a él, detenerse una fracción de tiempo y reemprender su movimiento, bien en la misma dirección, bien de vuelta hacia su origen, y en ambos casos ese punto es a la vez fin de un movimiento y principio de otro. Pero en un movimiento continuo el móvil no se detiene ningún tiempo en ningún punto, es decir, pasa por todos los puntos intermedios sin detenerse.

Las consideraciones anteriores le permiten a Aristóteles exponer otra refutación de la aporía del estadio de Zenón de Elea, de la que ya se había ocupado en el libro VI, donde la desarticuló estableciendo que la distancia y el tiempo pueden ser divididos potencialmente en un ilimitado número de partes. Ahora, yendo a la realidad del tiempo como magnitud unitaria y continua y basándose en la distinción entre potencia y acto establece que un infinito potencial puede ser recorrido, pero no un infinito en acto. Dicho de otra manera, si consideramos la trayectoria de un móvil como formada potencialmente por un número ilimitado de partes podemos considerar ese movimiento como continuo; pero la pretensión de considerar la trayectoria dividida actualmente en un número ilimitado de partes la descompone en un conjunto de movimientos sucesivos, impidiendo considerar el movimiento como uno y continuo.

En el tiempo, uno y continuo, los ahoras son los puntos límites e intermedios entre el antes y el después. Pero esos ahoras no son unidades mínimas de tiempo, como sostuvieron los pitagóricos, sino cortes sin dimensión en el tiempo, tal como los puntos son cortes de una línea. Solo así puede considerarse que el movimiento es continuo; en la perspectiva pitagórica el tiempo es la sucesión de un conjunto ilimitado de átomos temporales, y en cuanto tal no sería una magnitud continua, sino sucesiva, lo que sería igualmente extrapolable al movimiento. La extrapolación inversa no sería correcta: de la continuidad del tiempo no se deduce la continuidad de todo movimiento, sino tan solo su sucesividad.

No hay imposibilidad lógica en que el movimiento rotatorio sea uno y continuo, pues con el mismo impulso va desde cualquier punto de su trayectoria hacia sí mismo, sin que haya movimientos contrarios ni opuestos. Contrarios son los movimientos en ambas direcciones entre los extremos de una recta; contradictorios son los movimientos en ambas direcciones en una misma línea. Nada impide, pues, que el rotatorio sea un movimiento continuo sin interrupción alguna, ya que siempre está yendo desde sí mismo hacia sí mismo. La trayectoria del movimiento rotatorio no tiene límites definidos; sí los tienen, en cambio, el movimiento rectilíneo, o el que recorre un semicírculo o cualquier otro arco de círculo, por lo cual debe haber en ellos movimientos contrarios u opuestos, y en consecuencia no pueden ser continuos; en ellos el punto de partida no coincide con el punto final del movimiento.

Tampoco los demás tipos de movimiento pueden ser continuos, pues han de pasar repetidamente por puntos intermedios con movimientos contrarios; en el caso de las alteraciones habría que pasar por las etapas intermedias; en el caso de los cambios cuantitativos habría que pasar por sus grados intermedios; y lo mismo ocurre para la generación y destrucción. Aristóteles concluye su argumentación rechazando la doctrina de los fisiólogos antiguos que afirmaban que todas las cosas sensibles estaban siempre en movimiento, influidos por la preeminencia que daban al movimiento de alteración sobre los demás.

3. El movimiento rotatorio es el primordial

El movimiento rotatorio es anterior al rectilíneo, y ambos son anteriores al movimiento mixto, compuesto de ambos. Lo segundo es obvio y lo primero se debe a que el rotatorio es un movimiento más simple y más completo que el rectilíneo. Aristóteles lo argumenta así: por una parte, el movimiento rectilíneo infinito es imposible, pues el universo es limitado, pero incluso si existiera una recta infinita no podría ser recorrida por ningún móvil finito; por otra parte, el movimiento sobre una recta finita o vuelve sobre sí mismo y en ese caso realmente es un movimiento doble, o no vuelve sobre sí y en ese caso es incompleto y perecedero. Lo completo es anterior a lo incompleto y lo indestructible a lo destructible, en el orden de la naturaleza, de la razón y del tiempo; asimismo, el movimiento local eterno tiene prioridad sobre el que no lo es.

Esa conclusión, añade Aristóteles, es razonable, porque en el movimiento rectilíneo se pueden distinguir el punto inicial, los intermedios y el final, de modo que en el primero y el último el móvil está en reposo. Por el contrario, en el rotatorio no hay tales puntos definidos: todos ellos pueden ser considerados como iniciales, medios y finales. Por eso, de algunas cosas puede decirse a la vez que siempre están en el inicio y nunca están en el inicio, y que siempre están en el final y que nunca están en el final. De modo que de la esfera celeste puede decirse a la vez que está en reposo y en movimiento; lo primero porque ocupa siempre el mismo lugar, lo segundo porque gira en torno a la Tierra como centro. En el movimiento rotatorio puede decirse que el centro es el punto de inicio, el medio y el final.

Esa conclusión, añade Aristóteles, es razonable, porque en el movimiento rectilíneo se pueden distinguir el punto inicial, los intermedios y el final, de modo que en el primero y el último el móvil está en reposo. Por el contrario, en el rotatorio no hay tales puntos definidos: todos ellos pueden ser considerados como iniciales, medios y finales. Por eso, de algunas cosas puede decirse a la vez que siempre están en el inicio y nunca están en el inicio, y que siempre están en el final y que nunca están en el final. De modo que de la esfera celeste puede decirse a la vez que está en reposo y en movimiento; lo primero porque ocupa siempre el mismo lugar, lo segundo porque gira en torno a la Tierra como centro. En el movimiento rotatorio puede decirse que el centro es el punto de inicio, el medio y el final.

4. El primer motor no tiene magnitud

La última tesis que intenta demostrar Aristóteles en el libro VIII de la Física es que el primer motor no tiene partes ni magnitud. Empieza precisando que nada finito puede mover algo durante un tiempo infinito, porque la relación entre el movimiento del motor, el del móvil y el tiempo es tal que o los tres son finitos o los tres son infinitos, no hay más posibilidades. Esto encaja en una tesis más general: No es posible que una magnitud finita tenga una potencia infinita. Y también es verdadera la tesis alterna: En algo infinito no puede haber una potencia finita. Los argumentos para probar ambas tesis se basan, dicho en términos actuales, en que las magnitudes finitas y las infinitas no son arquimedianas.

A continuación Aristóteles se plantea el problema del movimiento violento de los proyectiles, donde no está claro de qué modo se cumple el principio de que todo lo que se mueve es movido por algo. Platón, en el Timeo, había dado a ese fenómeno y otros similares, como la respiración y la transmisión del sonido la siguiente explicación: como no hay vacío el movimiento de cualquier cosa mueve a otras con la que está en contacto y estas a sus contiguas, sucesivamente; es decir, la mano que arroja la piedra y esta misma a lo largo de su movimiento mueven al medio en que se mueve el móvil –aire, agua- de tal modo que el propio medio, como reacción, mueve al móvil. Esta teoría es conocida por el nombre de “antiperistasis” o mutua sustitución y Aristóteles la reformula teniendo en cuenta el fenómeno que actualmente llamamos rozamiento. La potencia motriz inicial del movimiento se va perdiendo a lo largo de la transmisión a los intermediarios continuadores del movimiento, hasta llegar un momento en que el último intermediario es movido, pero ya no tiene capacidad de mover, y entonces se acaba el movimiento.

En este punto Aristóteles resume su línea argumental así: a) En el universo hay un movimiento continuo; b) ese movimiento es uno y simple; c) ese movimiento tiene que ser el de una magnitud; d) esa magnitud ha de ser simple y movida por un motor que sea uno; e) ese motor simple está en movimiento o inmóvil; f) si está en movimiento entonces ha sido movido por algo, como todo lo que se mueve, y retrocediendo en la serie de movimientos se llega al movimiento que ha sido producido por algo inmóvil; g) este motor inmóvil no cambia al mover lo que mueve; h) lo movido por el motor inmóvil tampoco cambia al ser movido; i) como consecuencia de los dos puntos anteriores el movimiento que produce el motor inmóvil sobre lo movido por él es uniforme; j) el motor inmóvil debe ocupar el centro o la circunferencia (la superficie exterior) de la esfera, puesto que estos son los primeros principios de la esfera; k) las cosas más cercanas al motor inmóvil son las que se mueven con mayor velocidad, luego el motor inmóvil está en la circunferencia.

Toca plantearse ahora si el movimiento de la esfera sobre lo que mueve es continuo y uno o un conjunto sucesivo de movimientos; tanto si el movimiento es por impulso y atracción como si es por “antiperistasis” o movimiento mutuo de las partes del medio en que se produce, tal movimiento no puede ser uno y continuo, sino sucesivo y plural. De modo que el único movimiento continuo es el que produce el motor inmóvil sobre la esfera, porque la relación entre ambos se mantiene invariable y continua.

Para Aristóteles es evidente que el primer motor no puede tener magnitud, ni finita ni infinita. En efecto, ya en el libro III había demostrado que no puede haber magnitudes infinitas y ahora acaba de demostrar la imposibilidad de que una magnitud finita tenga una potencia infinita, como sería el caso de una cosa movida por una magnitud finita durante un tiempo infinito. Ahora bien, dado que el primer motor mueve con un movimiento eterno durante un tiempo infinito queda claro que no tiene magnitud, y en consecuencia, es indivisible y sin partes.

Actividades

1. Exponer la primacía del movimiento local sobre los demás tipos de movimiento desde la perspectiva del tiempo y desde el punto de vista de la continuidad.
2. Justificar por qué un movimiento rectilíneo no puede ser continuo, pero un movimiento rotatorio sí puede serlo.
3. Exponer las dos respuestas de Aristóteles a la aporía del estadio de Zenón de Elea.
4. Explicar la crítica aristotélica a la concepción pitagórica de los átomos de tiempo.
5. Argumentar la tesis aristotélica de que lo indestructible es anterior a lo destructible en el orden de la naturaleza, de la razón y del tiempo.
6. Explicar los argumentos que llevan a Aristóteles a decir que en el movimiento rotatorio puede decirse que el centro es un punto inicial medio y final.
7. Explicar la reciprocidad que establece Aristóteles entre la primacía del movimiento rotatorio celeste y la medida terrestre del tiempo.
8. Razonar el apoyo que encuentra Aristóteles en filósofos anteriores respecto a su tesis sobre la primacía del movimiento local sobre los demás tipos de movimiento.
9. Exponer la tesis de Platón sobre el movimiento de proyectiles y la corrección de su tesis por Aristóteles.
10. Exponer el razonamiento que lleva a Aristóteles a concluir que el motor inmóvil no tiene partes.

Para saber más

• "Aristóteles: la Física", en Historia de la Geometría Griega, Hernández. González, Miguel. Fundación Canaria Orotava de Historia de la Ciencia, 1992.
• Física, Aristóteles, Ed. Gredos; véase la introducción de G. de Echandía.
• Aristóteles, W. D. Ross, Ed. Charcas; véase el capítulo III.
• Los inicios de la ciencia occidental, David Lindberg, Ed. Paidós, véase cap. 3.
• El mundo físico de los griegos, Samuel Sambursky, Ed. Alianza.
• Diccionario Akal de El saber griego, J. Brunschwig y G. Lloyd